lattice_based_cryptanalysis

Lattice-Based Cryptanalysis Link 是一款用于格密码分析的工具包。

0x1 简介

格攻击过程可以抽象成以下的模型：

image-20240530215556948

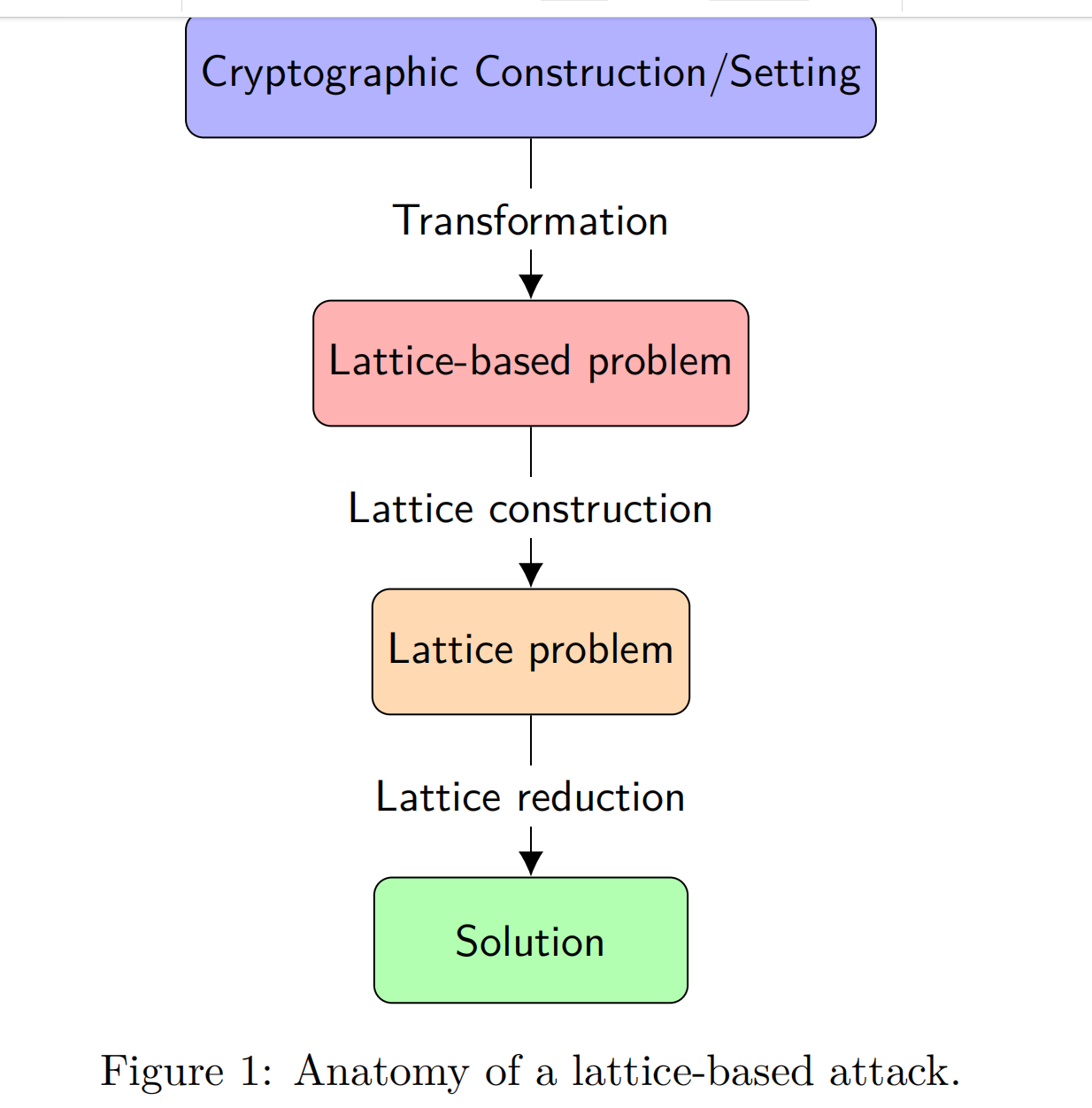
以一些常见的模型为例：

image-20240530215808323

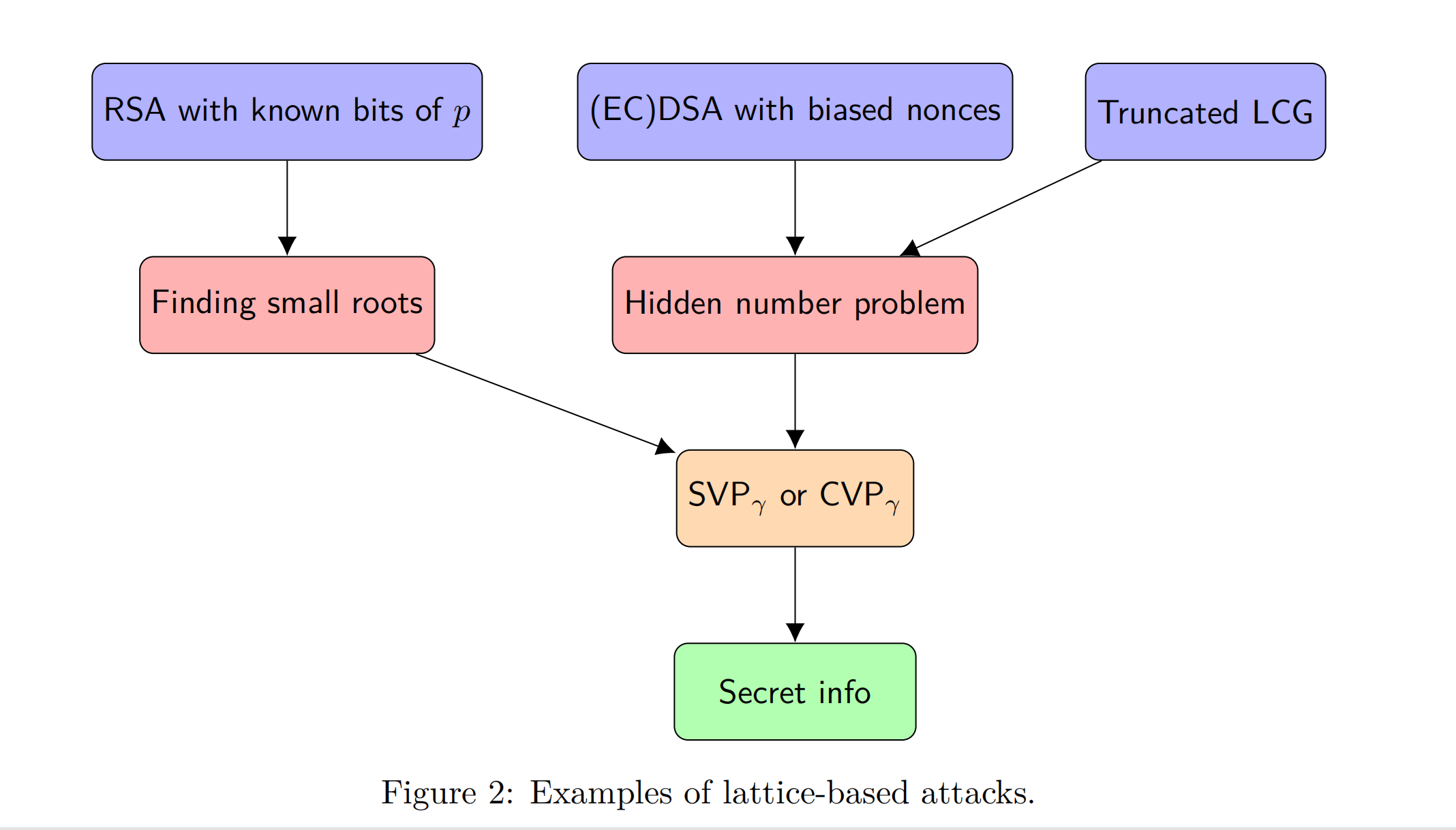
安装工具包：https://github.com/josephsurin/lattice-based-cryptanalysis

0x02 背景

2.1 基本定义

(Lattice)格：一个 n 维的格式欧式向量空间 的一个离散子群。

一个格可以被描述为整数域 上n个d维线性无关向量组成的基： 其中n被称为格的秩。

image-20240530221120517

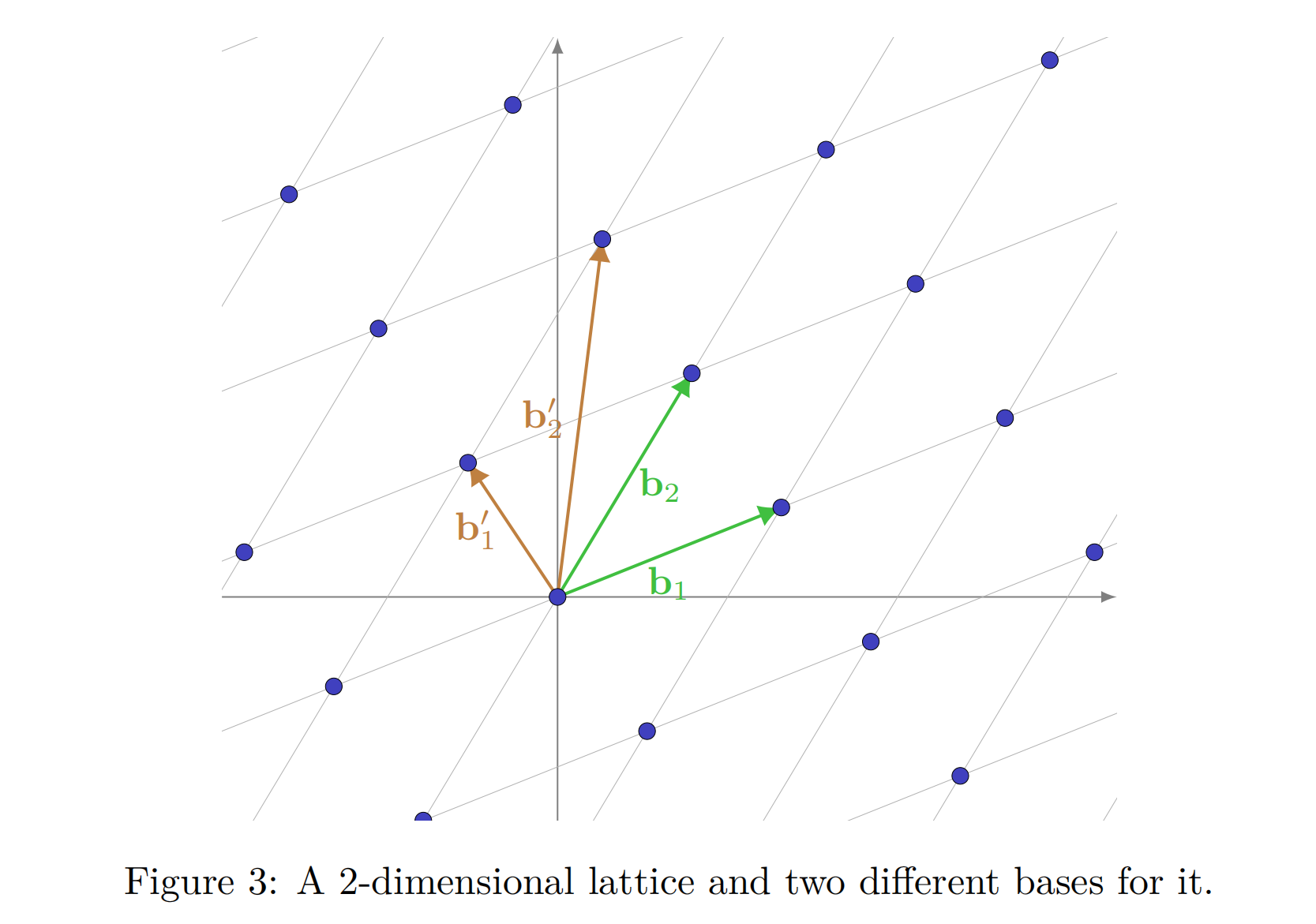
上图展示了二维的格，其中两组不同的基构成了相同的格。每个格都有无数个基，但只有某些特别”好“的基才可以用来解决特定问题。

(Fundamental Parallelepiped)格的基本域：令 为一个格。则B的基本域表示为

上图是 基本域的例子。事实上，一种判定 上的基是否是格基的方法是：检查格的基本域的覆盖范围是不是只包含格中的零点。

(Determinant)格的行列式：令B为满秩格L的基L=L(B)，则L的行列式 ，也被称为基本域 的n维体积，可以形式化表示为 当L是满秩格时，B是个方阵，有特殊形式 ​ 。

这里有个结论：两个基B和B'表示相同的格，当且仅当 ，其中U为 的整数矩阵。

(Successive Minima)：对任意n维格L， 为包含至少i个线性无关格点的最小的半径。

image-20240530231606022

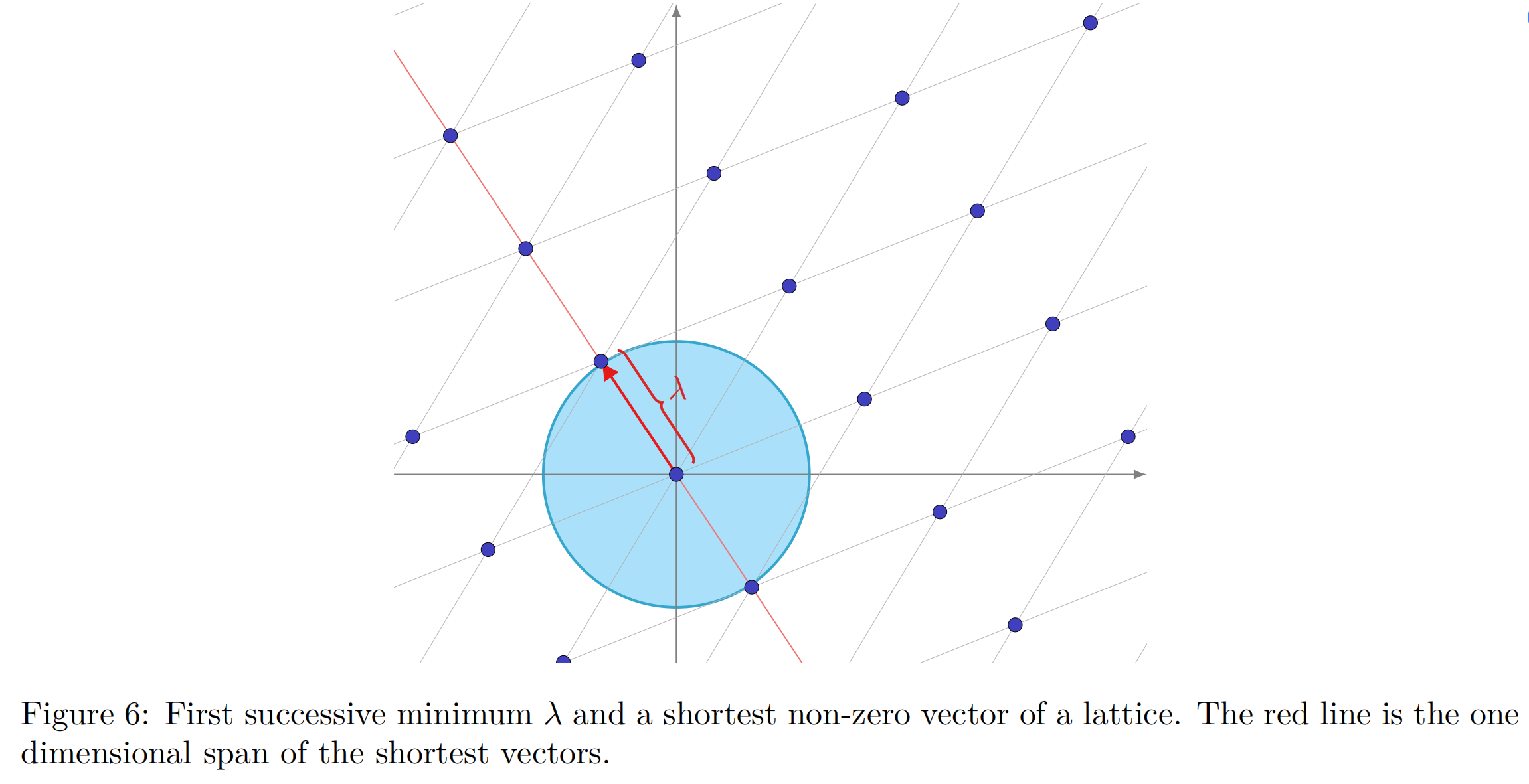
上图表示了一个格的 Successive Minima 的首项。对于一个格，高效的求 Successive Minima 的算法并不存在。但 Minkowski 给出了它的上界。

(Minkowski’s First Theorem)令L是n维满秩格。则

2.2 基于格的问题

(Shortest Vector Problem, SVP)最短向量问题：给定一个基为B的格L=L(B)，求非零格向量v满足 ​ 。

image-20240531112527491

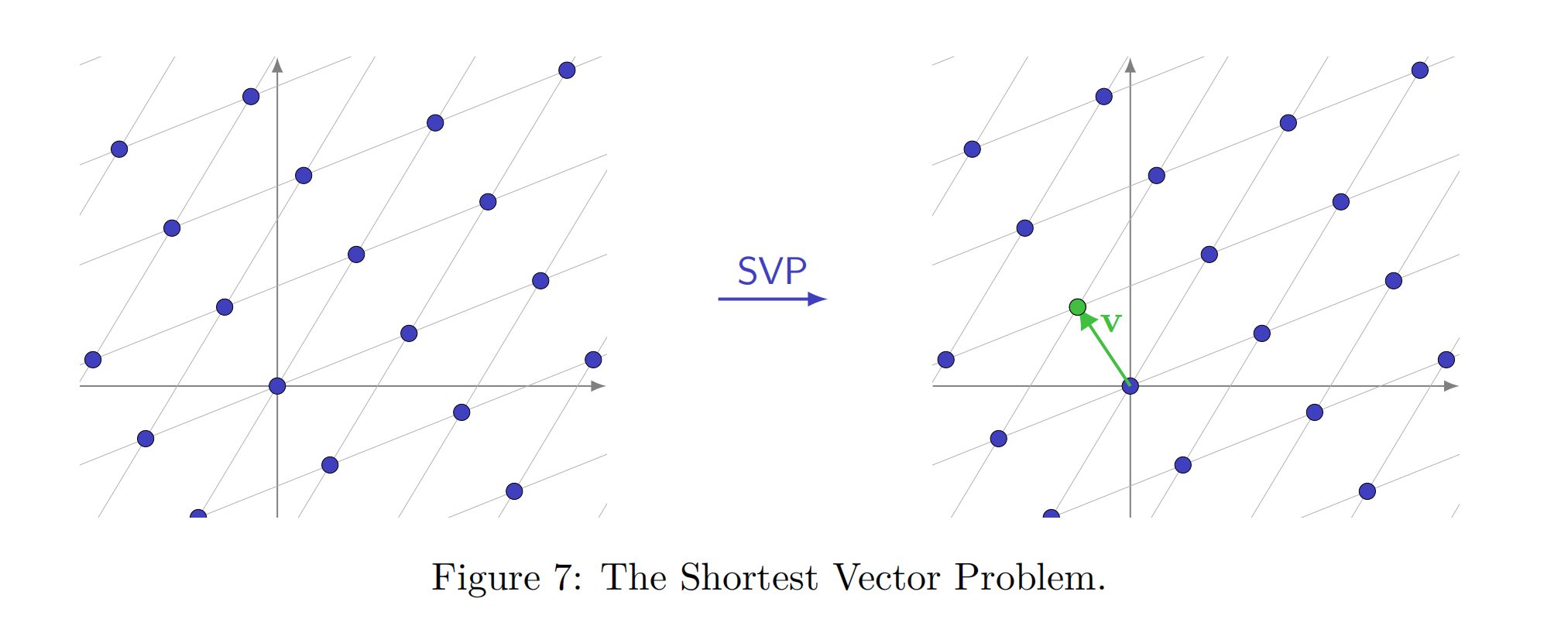
(Closest Vector Problem：CVP)最近向量问题：给定一个基为B的格L=L(B)，和一个目标向量t，求非零格向量v满足 ​ 。

image-20240531112545809

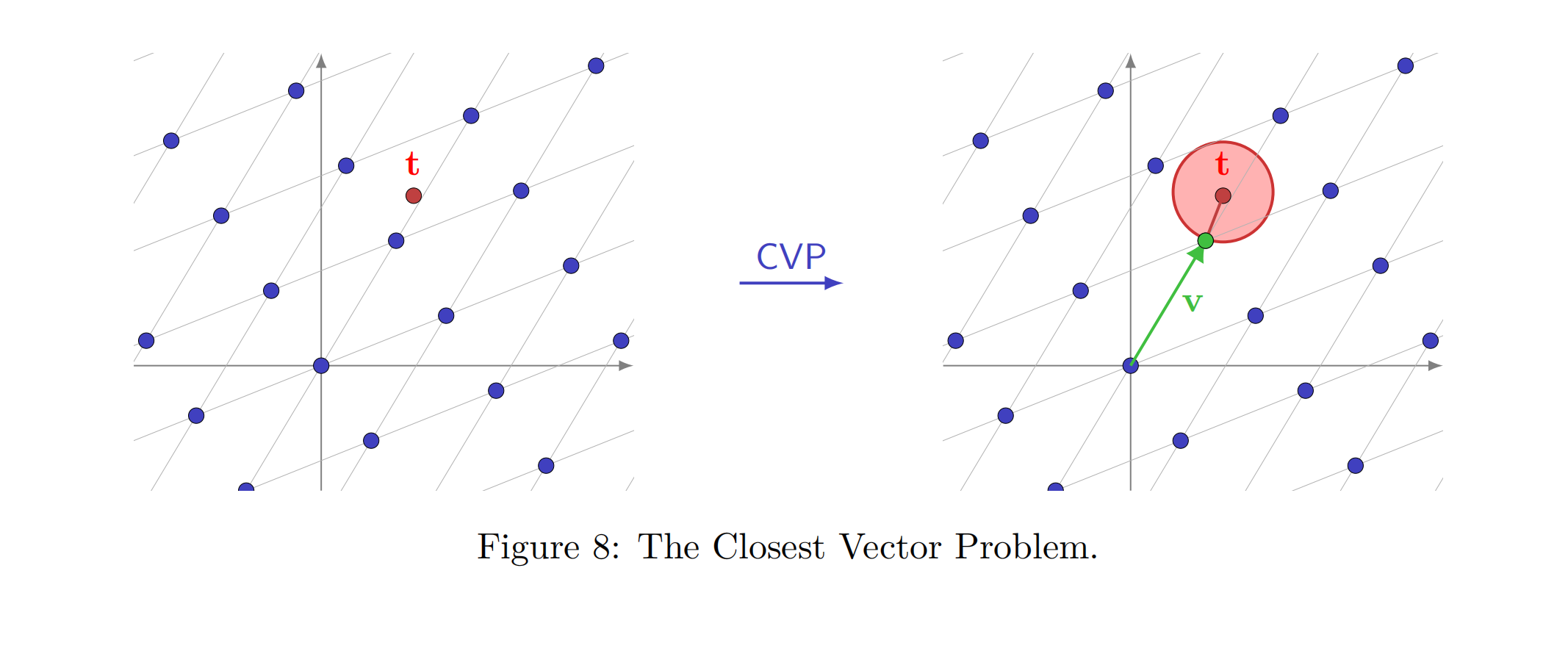
此外还有近似SVP, CVP问题，就是在SVP/CVP基础上加了一个参数。

image-20240531112708874

2.3 格的规约

由前面提到的结论，和基础的线性代数知识，可以推导出对格基的两种等价变换：向量行互换，向量行线性相加。LLL 算法和 Babai 算法就是基于这个结论对格基进行变换的。

LLL算法：

image-20240531213444569

这个算法的第一步是对格基进行 Gram-Schmidt 正交化过程的计算，以便后续对格基规约。Gram-Schmidt 的结果，包括正交向量b1*->bn*，和参数ui,j。它们满足：

image-20240531214609182

image-20240531214654153

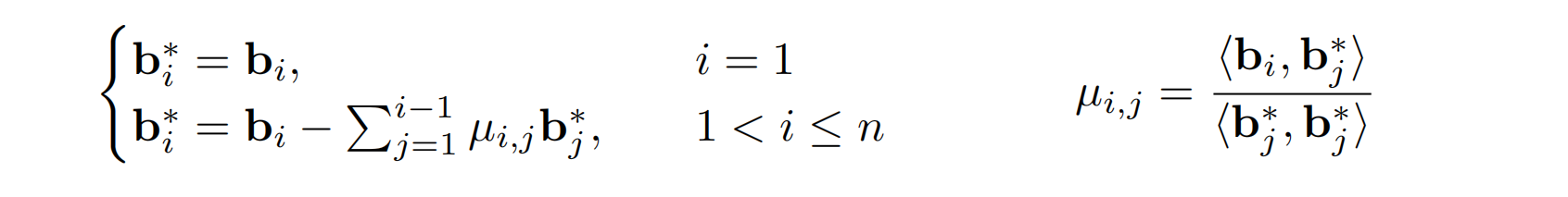
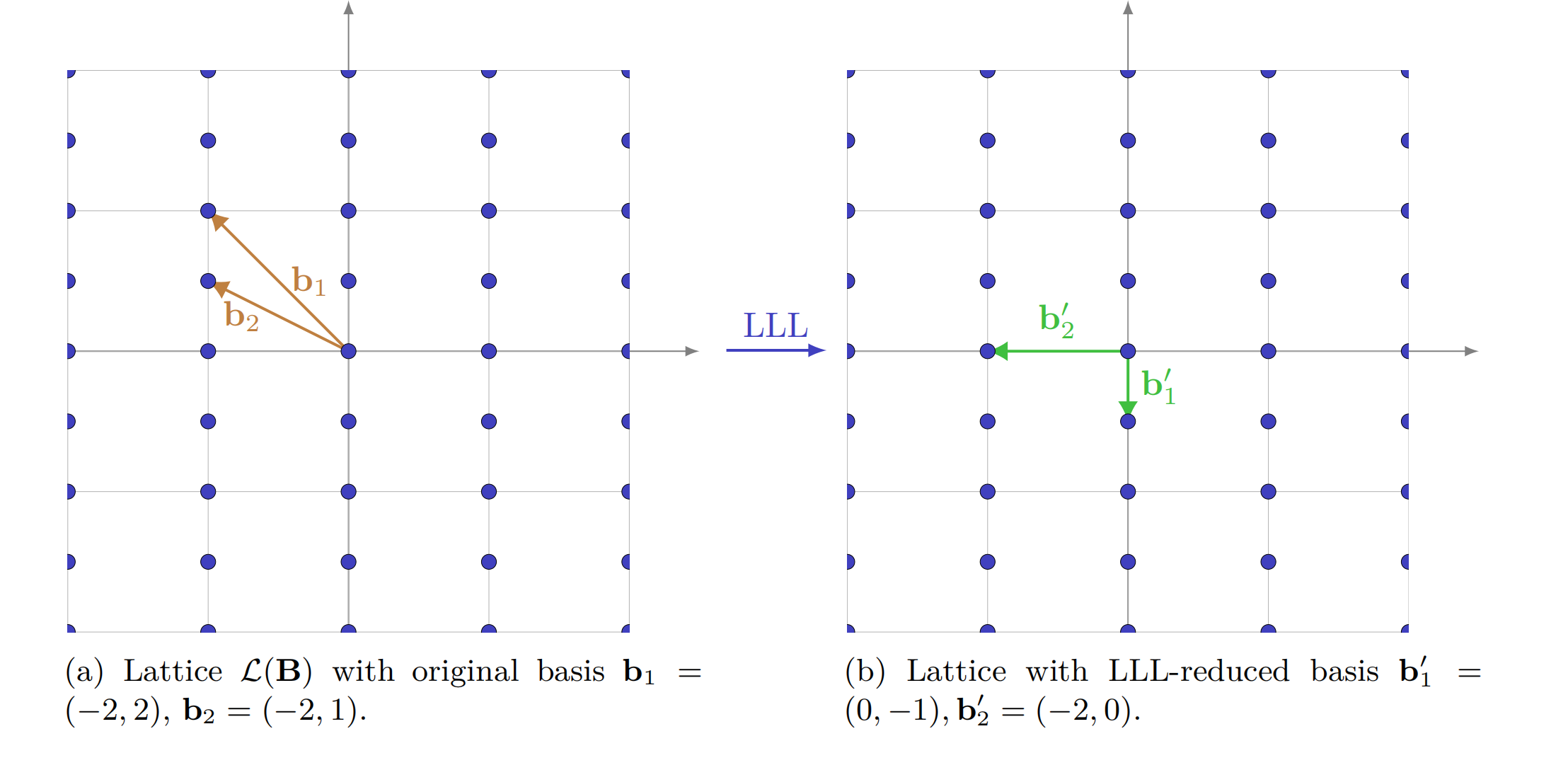
上图可以直观的看出 LLL 算法的作用：在格中找到最短向量。且具有下面的性质：

image-20240531214807529

image-20240531214915173

是 LLL 算法的近似参数。

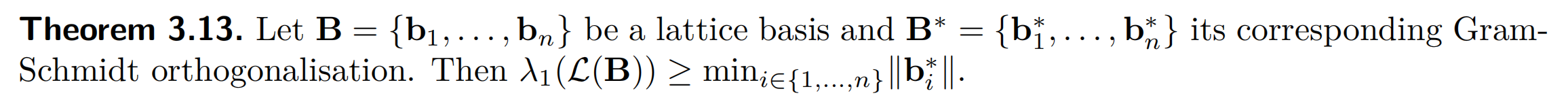
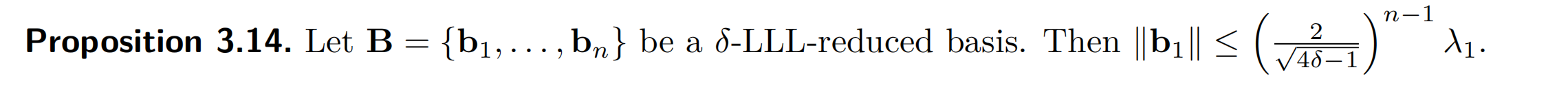
Babai 平面近似算法：输入秩为n的格L的一组基B和一个目标向量t，输出CVP问题的近似解。

image-20240531215106746

2.4 格规约的应用

格规约的简单应用是求实数的最小多项式。

(Minimal Polynomial)最小多项式：令a为实数，则a的最小多项式为最高次系数为1(以下简称首一)，次数最低，且其中一个根为a的多项式F(x)。